前言：本题来着[字节校园] 双月模拟笔试 3-4月场，个人感觉这是一个质量很高的题所以想要记录并分享一下自己当时的解法

Flowers

题面描述：给定 NN 个数 h1, h2, ... hnh_1,\ h_2,\ ...\ h_n 表示高度，和 NN 个数 a1, a2 .. ana_1,\ a_2\ ..\ a_n 表示高度对应的价值，求在高度序列中找到一串高度上升子序列使得价值最大，并输出最大价值

题目链接：Flowers

方法1： O(nlog⁡n)O_{(n\log{n})}

思路：

本题很容易让人联想到最长不上升子序列问题，结合数据范围应该是 贪心+二分 优化版最长上升子序列问题（详细参考：动态规划习题集)）。但是具体细节还没想地太明白这里就不讲解（欢迎大大们教教你们的做法）

但是，本题其实还可以用树状数组解决：

  1. 首先分析题干得到本题的重要信息：序列具有最优子结构的特性即子问题的最优解可以推导得到更大规模问题的解，这是使用动态规划解题的很重要的条件之一，而本题虽然不是使用动态规划解决但是这个性质对解题过渡很重要；

  2. 考虑 f[i][j]f[i][j] 表示在考虑前 ii 个销售员（花）并且身高为j的销售员作为身高上升子序列的最后一个元素所得到的最大价值

  3. 我们注意到对已经求 f[i][j]f[i][j] 就是要求 f[i−1][0]、f[i−1][1]、...、f[i−1][j−1]f[i-1][0]、f[i-1][1]、...、f[i-1][j-1] 中的最大值记做 f[i−1][k]f[i-1][k] 则 f[i][j]=f[i−1][k]+a[i]f[i][j] = f[i-1][k] + a[i]

  4. 这样我们就列出“转移方程 ” ：f[i][j]=max(f[i−1][0], f[i−1][1], ... f[i−1][j−1])+a[i]f[i][j] = max(f[i-1][0],\ f[i-1][1],\ ...\ f[i-1][j-1])+a[i] ， 到这里还是很容易想到的，于是对于数据范围较小的情况而言可以使用遍历法求得 maxmax 于是这就是一个典型的动态规划问题了，但是实际上本题的数据范围为 2e52e5 对于遍历法 On2O_{n^2}​​ 的复杂度而言是会超时的

  5. 我们现在考虑空间换时间的策略，使用两维长度都为 N+1N+1 的二维数组 arrarr ，而 arr[i][j]arr[i][j] 表示在考虑前 ii 个销售员（花）的情况下，身高小于数组下标（这里有一个特别的条件及时身高 1≤hi≤N1 \leq h_i \leq N 并且身高都不相同即这里的 hih_i 就是取满了 1∼N1 \sim N 内的所有数，也就可以将身高当做数组下标来用的，否则还需要进行身高排序后离散化处理）的身高不下降子序列所取到的最大价值（动态规划中的子状态）

  6. 现在考虑维护了 arrarr 数组后的“状态转移方程”： f[i][j]=arr[i−1][h[i]−1]+a[i]f[i][j] = arr[i-1][h[i]-1] +a[i] ，显然这里相比起前面的转移方程简单了，但是这里我们还要考虑 arrarr 数组的维护：arr[i][j]=f[i][j]arr[i][j] = f[i][j] 很显然，但是更新 arr[i][j]arr[i][j] 后还需要更新 arr[i][k] (k>h[i])arr[i][k]\ (k > h[i]) 并且 arr[i][k]=max(arr[i−1][k], f[i][j])arr[i][k] = max(arr[i-1][k],\ f[i][j]) 而 arr[i][t]=arr[i−1][t] (t<h[i])arr[i][t] = arr[i-1][t]\ (t < h[i]) ，我们可以注意到这里起始还是回到了 On2O_{n^2} 的做法

  7. 前面的朴素做法理解后我们可以来想一下优化的做法

  8. 首先，我们可以吸取动态规划问题中的状态压缩的思想（这个思想在背包问题中很常见，如不熟悉可以复习一下01背包问题）可以压缩掉 ff 和 arrarr 表示考虑前 ii 个销售员的第一维但是前提是需要数组初始化为0，这代表着在没有考虑任何销售员前提下所有的子序列的价值都为0

  9. 然后，考虑最影响复杂度的 arrarr 数组的维护问题， arrarr 数组存在的作用是查询区下标在 1∼h[i]−11 \sim h[i]-1 内最大的 ff，然后在求得 arr[h[i]]arr[h[i]] 后，通过 arr[h[i]]arr[h[i]] 的更改来更新下标在 h[i]∼Nh[i] \sim N 内的所有 arrarr​ 值

  10. 这样我们就抽象出来了两个操作 单点修改 和 区间查询 ，这里维护的值就是区间内的最大值

  11. 这样我们其实可以发现这是一个典型的维护区间最大值的线段树题了，但是实际上这里了还可以用比线段树更简单的数据结构——树状数组解决，因为这里的 arrarr 维护的一直就是 1∼i1 \sim i 区间内的最大值，而如果这里需要维护的不是必定以 11 开头的区间的话这里就必须用到线段树解决了

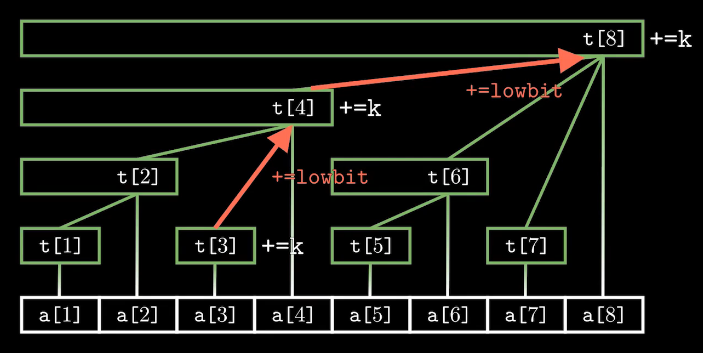
  12. 这里用tr树状数组维护arr，modify(x, d)操作就是指将arr[x]arr[x] 由 0 调整为 d 后tr对应的调整；query(x)操作就是指查询身高在 1 ~ x内的最大的f，对树状数组不太熟悉的可以参考一下树状数组

    树状数组-add.png

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;

typedef long long LL;

int n;
vector<int> h, a;
vector<LL> tr;

inline int lowbit(int x) {
	return x & -x;
}

void modify(int x, LL b) {
	for (int i = x; i <= n; i += lowbit(i)) {
		tr[i] = max(tr[i], b);
	}
}

LL query(int x) {
	LL ans = 0;
	for (int i = x; i; i -= lowbit(i)) {
		ans = max(ans, tr[i]);
	}
	return ans;
}

int main() {
	cin >> n;
	h.resize(n);
	a.resize(n);
	tr.resize(n + 10);
	for (int i = 0; i < n; i++)
		cin >> h[i];
	for (int i = 0; i < n; i++)
		cin >> a[i];

	LL ans = 0;
	for (int i = 0; i < n; i++) {
		LL t = query(h[i]) + a[i];
		ans = max(ans, t);
		modify(h[i], t);
	}

	cout << ans << endl;
	return 0;
}