数学部分基础(4)
容斥原理
韦恩图:
整个图形的面积可以用:
- +
表示,这样可以合理推广得到这样的公式:
$S_1\ \cap \ S_2\ \cap \ …\ \cap S_n\ $ = c
$S_1\ +\ S_2 +\ …\ S_n $ - + - …+
第一行有 项, 第二行有 项,… , 第n行有 项
共有: = = = 项
实现:使用二进制表示的形式实现表示这 项的取法(避免使用DFS造成的额外空间浪费)然后按照所取的项数决定最终的加减符号取值
核心代码:
1 | for(int i = 1; i < 1 << m; i++){ |
简单博弈论
公平组合游戏 ICG
若一个游戏满足:
- 由两名玩家交替行动;
- 在游戏进程的任意时刻,可以执行的合法行动与轮到哪名玩家无关;
- 不能行动的玩家判负;
则称该游戏为一个公平组合游戏。
NIM博弈属于公平组合游戏,但城建的棋类游戏,比如围棋,就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子,胜负判定也比较复杂,不满足条件2和条件3。
有向图游戏
给定一个有向无环图,图中有一个唯一的起点,在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动,每次可以移动一步,无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是,把每个局面看成图中的一个节点,并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。
NIM游戏
描述:给定N堆物品,第i堆物品有Ai个。两名玩家轮流行动,每次可以任选一堆,取走任意多个物品,可把一堆取光,但不能不取。取走最后一件物品者获胜。两人都采取最优策略,问先手是否必胜。
概念:
必胜态:进行一步操作后一定会让对手处于必败态
必败态:进行任意操作对手都可以采取对应操作使其下一轮任然处于必败态
结论:
必胜态:a_1 \and a_2 \and ...\and a_n \ne 0
必败态:a_1 \and a_2 \and ...\and a_n = 0
论证:由于异或操作一定会使最终值比所有的值总最大的那一个更小,所以一定可以通过在最大的那一堆中取出适当的值使得必胜态转换为必败态;
并且当处于必败态后无论在那一堆中取值都会是得原来成偶对的01对(将视为二进制数组)变成成奇对的01对故对手可以采取措施使其再次返回必败态。
并且最终的结果是所有的堆中为0,也即必败态
故结论成立
实现:取所有数进行异或运算。
核心代码:
1 | int ans = 0; |
Mex运算
设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算,即:
mex(S) = min{x}, x属于自然数,且x不属于S
SG函数
在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1, y2, …, yk,定义SG(x)为x的后继节点y1, y2, …, yk 的SG函数值构成的集合再执行mex(S)运算的结果,即:SG(x) = mex({SG(y1), SG(y2), …, SG(yk)})
特别地,整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即SG(G) = SG(s)。
定理:
-
有向图游戏的某个局面必胜,当且仅当该局面对应节点的SG函数值大于0。
-
有向图游戏的某个局面必败,当且仅当该局面对应节点的SG函数值等于0。

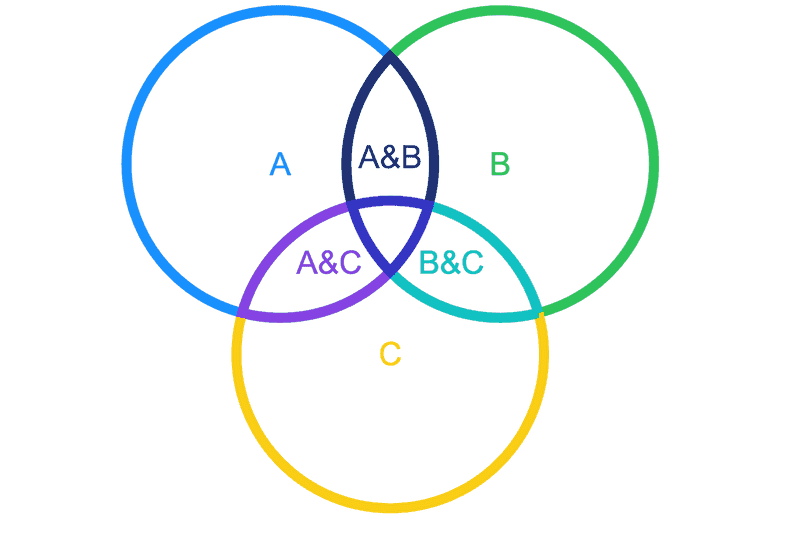


.jpg)
.jpg)